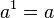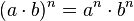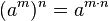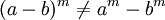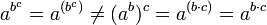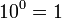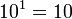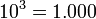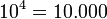6to Año. Propiedades de la radicación

Las propiedades de la radicación son bastante similares a las propiedades de la potenciación, puesto que una raíz es una potencia con exponente racional.

Ejemplo:

$\sqrt[4]{x^3}$ = $\ x^{3/4}$ .

Raíz de un producto

La raíz cuadrada de un producto A x B es igual al producto de la raíz cuadrada de "A" por la raíz cuadrada de "B"

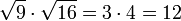
$\sqrt{3^2 \cdot 2^4}$ = $\sqrt{9} \cdot \sqrt{16} = 3\cdot 4 = 12$

o tambien se puede hacer de esta forma:

$\sqrt{3^2 \cdot 2^4} = \sqrt{9 \cdot 16} = \sqrt{144} = 12$

Raíz de un cociente

El cociente de la raíz de una fracción, es igual al cociente de la raíz del numerador entre la raíz del denominador....

$\sqrt[n]{\frac{a}{b}} = \frac{a^{1/n}}{b^{1/n}}$ = $\frac{\sqrt[n]{a}}{\sqrt[n]{b}}$

Ejemplo:

$\sqrt{\frac{9}{4}} = \frac{\sqrt{9}}{\sqrt{4}}$ = $\frac{3}{2}$

Cuando esta propiedad se hace con números no hace falta pasar la raíz a potencia de exponente racional, aunque sí cuando se hace con variables.

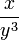
$\sqrt[3]{\frac{x^3}{y^9}} = \frac{x^{3/3}}{y^{9/3}}$ = $\frac{x}{y^3}$

Ejemplo:

$(\sqrt[4]{a^2})^8 = (\ a^{2/4})^8$ = $\sqrt[4]{a^{16}}$

Raíz de una raíz

Para calcular la raíz de una raíz se multiplican los índices de las raíces y se conserva la cantidad subradical.

$\sqrt[n]{\sqrt[m]{a}}$ = $\sqrt[n.m]{a}$

Ejemplo:

$\sqrt[7]{\sqrt[3]{5}}$ = $\sqrt[21]{5}$

6to Año.- Propiedades de la Potenciación

Potencia de exponente 1

Toda potencia de exponente 1 es igual a la base.

$a^1 = a \,$

ejemplo:

$54^1=54 \,$

Multiplicacion de potencias de igual base

El producto de dos o más potencias de igual a base «a» y el exponente igual a la suma de los correspondientes exponentes (la misma base y se suman los exponentes):

$a^m \cdot a^n = a^{m + n}$

ejemplos:

$9^3 \cdot 9^2 = 9^{3+2}= 9^5$

Division de Potencias de Igual Base

La división de dos potencias de igual base a es igual a la potencia de base a y exponente igual a la resta de los exponentes respectivos (la misma base y se restan los exponente = a (cero)

$\frac{a^m}{a^n}=a^{m - n}$

Potencia de un producto

La potencia de un producto es igual a cada uno de los factores del producto elevados al exponente de dicha potencia. Es decir, una potencia de base (a.b) y de exponente "n", es igual al factor "a" elevado a "n" por el factor "b" elevado a "n"

$(a \cdot b)^n=a^n \cdot b^n$

Potencia de una potencia

La potencia de una potencia de base a es igual a la potencia de base a elevada a la multiplicación de ambos exponentes (la misma base y se multiplican los exponentes):

$(a^m)^n = a^{m \cdot n}$

Propiedad distributiva

La potenciación es distributiva con respecto a la multiplicación y a la división:

$(a \cdot b)^n = a^n \cdot b^n$

$\Big(\frac{a}{b}\Big)^n = \frac{a^n}{b^n}$

pero no lo es con respecto a la suma ni a la resta.

Propiedades que no cumple la potenciación

No es distributiva con respecto a la adición y sustracción:

$(a + b)^m \neq a^m + b^m$

$(a - b)^m \neq a^m - b^m$

No cumple la propiedad conmutativa, exceptuando aquellos casos en que base y exponente tienen el mismo valor o son equivalentes.

En general:

$a^b \neq b^a$

Tampoco se cumple la propiedad asociativa:

$a^{b^c}=a^{(b^c)}\ne (a^b)^c=a^{(b\cdot c)}=a^{b\cdot c}$

Potencia de base 10

En las potencias con base 10, el resultado será la unidad seguida de tantos ceros como indica la cifra del exponente.

Ejemplos:

$10^0=1 \,$

$10^1=10 \,$

$10^2=100 \,$

$10^3=1.000 \,$

$10^4=10.000 \,$

$10^5=100.000 \,$

$10^6=1.000.000 \,$

6to Año - Números Reales - Simbología y propiedades

Propiedades de adición en el conjunto de los números reales

Sean $a\, \varepsilon \, I\! \! R, \,\, b\, \varepsilon \,I\! \! R$ entonces $a+b=b+a \hspace{0.5cm}$ (la adicción es conmutativa)

$\hspace{0.5cm}$ Por ejemplo:

Sean $a\, \varepsilon \, I\! \! R, \,\, b\, \varepsilon \,I\! \! R, \,\, c\, \varepsilon \,I\! \! R$ entonces $a+(b+c)=(a+b)+c \hspace{0.5cm}$ (la adición es asociativa)

Por ejemplo:

Existe $0,\, 0\, \varepsilon \, I\! \! R$ tal que para cada $a ,a\, \, \varepsilon \,I\! \! R,\,\, a+0=a \hspace{0.5cm}$ ( es el elemento neutro aditivo)

$\hspace{0.5cm}$ Por ejemplo: $\displaystyle{ {\frac{-3}{5}}+0={\frac{-3}{5}}}$

Para cada $a,\, a\, \varepsilon \, I\! \! R$ existe $-a ,-a\, \, \varepsilon \,I\! \! R$ tal que $a+(-a)=0 \hspace{0.5cm}$ (cada número real posee inverso aditivo)

$\hspace{0.5cm}$ Por ejemplo: el inverso aditivo de es pues

Propiedades de la multiplicación en el conjunto de los números reales

Sean $a\, \varepsilon \, I\! \! R, \,\, b\, \varepsilon \,I\! \! R$ entonces $a\cdot b=b\cdot a \hspace{0.5cm}$ (la multiplicación es conmutativa)

$\hspace{0.5cm}$ Ejemplo: $3\cdot 2=2\cdot 3$

Sean $a\, \varepsilon \, I\! \! R, \,\, b\, \varepsilon \,I\! \! R, \,\, c\, \varepsilon \,I\! \! R$ entonces $a\cdot (b\cdot c)=(a\cdot b)\cdot c \hspace{0.5cm}$ (la multiplicación es asociativa)

$\hspace{0.5cm}$ Ejemplo: $-5\cdot (2\cdot 1)=(-5\cdot 2)\cdot 1$

Existe $1;\, 1\, \varepsilon \, I\! \! R$ tal que para cada $a ,a\, \, \varepsilon \,I\! \! R,\,\, a\cdot 1=a \hspace{0.5cm}$ (

es el elemento neutro multiplicativo)

$\hspace{0.5cm}$ Ejemplo: $4\cdot 1=4$

Para cada $a,\, a\, \varepsilon \, I\! \! R, \, a\neq 0$ , existe $\displaystyle{ {\frac{1}{a}},\,\,{\frac{1}{a}}\, \, \varepsilon \,I\! \! R}$ tal que $\displaystyle{ a\cdot {\frac{1}{a}}=1} \hspace{0.5cm}$ (cada número real diferente de 0 posee inverso multiplicativo)

$\hspace{0.5cm}$ Ejemplo: $15\cdot \displaystyle{ {\frac{1}{15}}} =1$

Propiedad distributiva de la multiplicación con respecto a la adición

Si $a\, \varepsilon \, I\! \! R, \,\, b\, \varepsilon \,I\! \! R, \,\, c\, \varepsilon \,I\! \! R$ entonces se cumple que:
$\begin{displaymath}a\cdot (b+c)=a\cdot b+a\cdot c\end{displaymath}$